
What are the Kinematic Equations?
The kinematic equations are a set of equations that describe the motion of an object with constant acceleration. Kinematics equations require knowledge of derivatives, rate of change, and integrals. To keep our focus on high school physics, we will not be covering integrals.
When we use the kinematic equations, we use specific notation to denote initial and final measurements. For example, when we have an initial velocity value, it is written as $ \Large\mathcal{v}_{\normalsize0} $. When we write the final velocity, we simply write $ \Large\mathcal{v} $, without a subscript. Therefore, the change in the velocity of the object is represented by the equation $ \Delta\Large\mathcal{v} = \mathcal{v} - \mathcal{v}_{\normalsize0} $. This notation also applies to displacement and time. This means $ {\large x}_0 $ is the initial position, $ {\large x} $ is the final position, $ {\large t}_0 $ is the initial time, and $ \large t $ is the final time. It’s important to remember that the initial time, $ {\large t}_0 $, will equal zero for kinematics equations. Because the time interval is $ \Delta\mathcal{t} $ and $ {\mathcal{t}}_0 = 0{\normalsize{s}} $, we know that $ \Delta\mathcal{t} = \mathcal{t} $.
How Can I Choose the Right Equation?
The kinematic equations can be applied to a variety of dimensional motion problems that consider the motion of an object with constant acceleration. When problem-solving, the formula we choose should include the unknown variable, as well as three known variables. Each of the equations is missing one variable. This allows you to identify what variable is not given or asked for in your problem, before selecting the equation that is also missing that variable. Let’s take a closer look.
Missing displacement? This formula is missing $ \Delta{\large x} $ and should be used for problems that do not include or ask for displacement.
$ \Large v = v_0 + \Large {at} $
Missing acceleration? This formula is ideal for problems that do not include or ask for acceleration. However, it’s important to remember that sometimes acceleration is indirectly referenced, such as when an object is in free fall (see below).
$ \Large \Delta \large x = \LARGE (\frac {v + v_0}{2}) \large t $
Missing final velocity? This formula can be used when the problem does not mention or ask for final velocity. Sometimes final velocity is indirectly referenced. When the problem includes, “comes to a stop” or “before stopping”, $ \large v = \normalsize 0 \textrm {m/s} $. This equation often utilizes the quadratic formula during problem-solving.
$ \Large{\Delta{\large x} = \LARGE v_{\normalsize{0}} \large t + \frac {1}{2}at^2} $
Missing time? When the problem does not give a time interval, choose this equation.
$ \LARGE v^2 = {v \normalsize{_0}}^2 + \Large 2a\Delta{\large x} $
Velocity, Acceleration, and Air Resistance
When we use the kinematics equations, we can make some mathematical assumptions. When an object in motion moves through the air, air resistance slows the object’s speed. Luckily, when we use the equations of motion, we assume air resistance is insignificant enough to ignore.
The second assumption we can make when using these equations involves acceleration. We already know that acceleration is constant for kinematics problems, which means that the average acceleration is equal to this value. Objects in free fall, or projectiles, all experience the same acceleration, regardless of their mass. This means that whenever an object is thrown, dropped, or falling, it moves with a constant downward acceleration of $ 9.81 \textrm {m/s}^2 $. It is important to remember that this value is a magnitude. If we assume upwards to be a positive direction or y value, then an object falling downward will have a negative acceleration of $ -9.81 \textrm {m/s}^2 $.
Because kinematics equations are used when the acceleration of the object is constant, we can use a simple equation to determine the average velocity of an object. To find the average velocity, simply add the initial velocity to the final velocity and divide by 2.
$ \LARGE v_{ \textrm {average}} = \bar{v} = \frac {v_1 + v_2}{2} $ This equation can only be used when acceleration is constant
When an object moves in a straight-line motion along the x-axis, we can use the displacement of an object and the time interval to determine the average velocity. This equation considers initial position, final position, and the time interval.
$ \LARGE v_{ \textrm {average}} = \bar{v} = \frac { x_2 - x_1}{ t_2 - t_1} = \frac {\Delta x}{\Delta t} $
You can use the slope of a line tangent to the position-time cure to determine the velocity of the object. The velocity of an object at a specific point in time is called instantaneous velocity. Graphing a position-time graph can help you to determine both instantaneous velocity and average velocity. Similarly, graphing a velocity-time graph can help you determine the instantaneous acceleration and average acceleration of an object because acceleration is the rate of change of velocity. However, when we apply this to the kinematics equations, which have constant acceleration, an object’s instantaneous acceleration will be equal to its average acceleration.

How to Derive the Kinematics Equations
The First Equation: $ \large v = v_0 + at $
1.) To begin deriving the first kinematic equation, we should first consider the definition of acceleration.$ \Large a = \frac {\Delta v}{\Delta t} $
2.) We know $ \Large \Delta v = v - v\normalsize{_0} $ , and when we plug that in, we get $ \Large a = \frac {v - v_0}{\Delta t} $
3.) If we solve for $ \Large v $, the equation becomes $ \Large v = v_0 + \Large a \Delta t $
4.) We can denote the time interval as 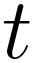 to generate the first kinematic equation.
to generate the first kinematic equation.
$ \LARGE v = v_0 + at $
The Second Equation: $ \Delta x = (\frac {v + v_{\normalsize0}}{2}) t $
To derive this equation, we’ll consider a velocity-time graph with constant acceleration. The slope of a velocity graph can be interpreted as acceleration and the area under the graph is equal to the object’s displacement, $ \Delta x $ .
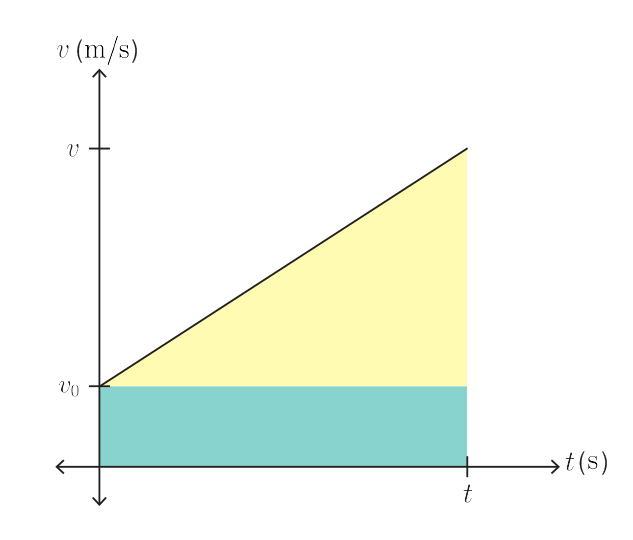
Here, the height of the blue rectangle is $ \large v_0 $ and the width is $ \large t $ so the area is equal to $ \large v_0 t $ .
The base of the red triangle is $ \large t $ and the height is $ \large v - v_0 $, so the area of the red triangle is $ \large \frac {1}{2} t (v - v_0) $ .
1.) When we sum the red and blue areas, we get $ \large \Delta x = v_0 t + \frac {1}{2} t (v - v_0) $
2.) When we distribute the factor of $ \large \frac {1}{2} t $ we get $ \large \Delta x = v_0 t + \frac {1}{2} vt - \frac {1}{2} v_0 t $
3.) We can simplify the equation by combining the initial velocity terms. $ \large \Delta x = v_0 t + \frac {1}{2} at^2 $
4.) Then, we further simplify the equation to get our second kinematic equation.
$ \LARGE \Delta x = (\frac {v + v_{\normalsize0}}{2}) t $
The Third Equation: $ \Delta x = v_0 t + \frac {1}{2} at^2 $
We can derive the third kinematic equation by plugging in the first kinematic formula into the second formula.
1.) Start with the second kinematic equation. $ \large \frac {\Delta x}{t} = (\frac {\Large v + v_{\normalsize0}}{2}) $
2.) Substitute the first kinematic formula for $ \large v $. $ \Large v = v\normalsize{_0} + \Large at $
3.) Once substituted, the equation becomes $ \large \frac {\Delta x}{t} = \frac {\Large (v_0 + at) + v_0}{2} $
4.) Expand the equation into $ \large \frac {\Delta x}{t} = \frac {\Large v_0}{2} + \frac {\Large at}{2} + \frac {\Large v_0}{2} $
5.) We can combine terms to simplify the equation into $ \large \frac {\Delta x}{t} = v_0 + \frac {\Large at}{2} $
6.) Finally, we can multiply both sides by time, $ \large t $, to generate our third kinematic equation.
$ \Large \Delta x = v_0 t + \frac {1}{2} at^2 $
The Fourth Equation: $ v^2 = {v_0}^2 + 2a \Delta x $
The fourth kinematic equation can be derived using the first and second kinematic equations.
1.) Start with the second kinematic formula. $ \large \Delta x = (\frac {v + v_{\normalsize0}}{2}) t $
2.) We can use the first kinematic formula, $ \Large \mathcal{v} = \mathcal{v}\normalsize{_0} + \large at $, to solve for time. $ \large t = \frac {\Large v - v_{\normalsize0}}{a} $
3.) We can plug our expression for time into the second kinematic formula. $ \large \Delta x = (\frac {\Large v + v_{\normalsize0}}{2}) (\frac {\Large v - v_{\normalsize0}}{\Large a}) $
4.) Next, we can multiply the fractions to simplify. $ \large \Delta x = \Large (\frac {v^2 + {v_{\normalsize0}}^2}{\large 2a}) $
5.) When we solve for $ \large v^2 $, we get our fourth kinematic equation.
$ \LARGE v^2 = {v_0}^2 + 2a \Delta x $

Problem-Solving for Kinematic Equations
When solving kinematics problems, there are steps you can follow to help structure your thought process. After reading the problem, draw a diagram, and label the knowns and unknowns. Identify what you are being asked to find. Then, identify the variables the problem provides. Next, determine which equations connect your known variables to your unknown variable. Then, you can begin solving.
Free Fall
In this problem, motion only occurs in the downward direction, so we'll make downward the positive direction. $ g = 9.81 \textrm {m/s}^2 $
We’ll use the third Kinematics equation for this problem. $ \Delta x = v_0 t + \frac {1}{2} at^2 $
We know that $ \large v_0 = \normalsize 0 \textrm {m/s} $. We can eliminate terms involving $ \large x_0 = v_0 = \normalsize 0 $, let $ \large a = g $ and $ \large x = h $. After completing the substitutions, we get the equation $ \large h = \frac {1}{2} gt^2 $
Next, we need to create an expression for time.
$ \large v = gt $ can be rearranged into a function of time $ \large t = \frac {v}{g} $
Then we can plug our equation for time into our simplified equation for height to get our answer.
$ \Large h = \frac {1}{2} gt^2 = \frac {1}{2}g (\frac {v}{g})^2 = \frac {v^2}{2g} = \frac {(10 \textrm {m/s})}{2(9.81 \textrm {m/s}^2)} = \large 5.1 \textrm m $
Teaching Tools
Wireless Photogate and Picket Fence
The Wireless Photogate improves on the designs of traditional photogates to provide students with real-time velocity data and enhanced features for more applications. From investigations in free fall and projectile motion to pendulums and cart collisions, the Wireless Smart Gate enables students to collect highly accurate motion data for a variety of objects.This problem only has motion occurring in the downward direction, so we can make downward the positive direction. $ g = 9.81 \textrm {m/s}^2 $
We know that $ \large x_0 = \normalsize 0 \textrm m $ and $ \large v_0 = \normalsize 0 \textrm {m/s} $.
We will use the kinematic equation $ \Delta x = v_0 t + \frac {1}{2} at^2 $.
We can eliminate terms, substitute $ \large a = g $, and assign $ \large h $ to height.
$ \large x = h $$ \large h = (0)t + \frac {1}{2} gt^2 $
Plug in our values for gravity and time to create the final equation.
$ \Large h = \frac {1}{2} gt^2 = \frac {1}{2}(9.81 \textrm {m/s}^2)(1 \textrm s)^2 = 4.9 \textrm m $

Linear Motion in One Dimension
What are the given values? $ \large v_0 = 5 \textrm {m/s} $ $ \large v_0 = 0 \textrm {m/s} $ $ \large x - x_0 = 23 \textrm m $
We can rearrange the second kinematics formula $ \Delta x = (\frac {v + v_{\normalsize0}}{2}) t $
Substitute our equation for $ \Delta x $ and rearrange the equation. $ x - x_0 = \frac {1}{2}(v_0 + v) t $
Arrange the equation to solve for $ \large t $, and plug in our known values to solve.
$ \Large t = 2 (\frac {x - x_0}{v_0 + v}) = 2 (\frac {23 \textrm m}{5 \textrm {m/s} + 0 \textrm {m/s}}) = \large 11.6 \textrm s $
Teaching Tools

Dynamics Cart and Track System
Dynamics Cart and Track Systems are multi-purpose equipment sets that enable educators to demonstrate and teach a variety of complex physics topics in Kinematics and Dynamics. Since their invention, PASCO’s dynamics systems have become essential tools in physics labs around the world. Our dynamics systems are complete experiment solutions that enable students to observe, measure and analyze motion through hands-on experimentation. Whether you’re new to dynamics systems, or you’re looking to enhance your current systems’ capabilities, we offer a range of customizable dynamics systems to fit your budget and needs.

List the known values. $ \large v_0 = 0 \textrm {m/s} $ $ \large v = 13 \textrm {m/s} $ $ \large x - x_0 = 150 \textrm m $
Start with the first kinematics formula $ \large v^2 = {v_0}^2 \normalsize + 2a \Delta x $ and plug $ \large x - x_0 $ in for $ \Delta x $.
$ \Large v^2 = {v_0}^2 + 2a (x - x_0) $
Rearrange the equation to solve for acceleration and plug in our known values, then solve.
$ \Large a = \frac {v^2 - {v_0}^2}{2(x - x_0)} = \frac {(13 \textrm {m/s})^2 - (0 \textrm {m/s})^2}{2(2.2 \textrm m)} = \large {38.0 \textrm {m/s}}^2 $

Linear Motion in the Second Dimension
Problems that include an inclined plane, ramp, or projectile will require us to split the motion into $ \small \overrightarrow{\normalsize x} $ and $ \small \overrightarrow{\normalsize y} $ vector components. Consider a jet with two perpendicular engines that propel it along the x and y axes. When only the vertically aligned engine is on, the jet is propelled along the y axis. Similarly, when only the horizontally aligned engine is on, the jet is propelled along the x axis. When both engines are on, the motion of the jet occurs in both the x and y directions, but neither x nor y affect one another. For this reason, we can analyze the $ \small \overrightarrow{\normalsize x} $ and $ \small \overrightarrow{\normalsize y} $ components for each vector separately, while recognizing that they are related by a shared $ \large t $ value. The directions of the components can be conveyed by assigning a plus or minus sign to each one.
| $ \LARGE x $ Component | $ \Large y $ Component |
|---|---|
| $ \large v_x = v_{0x} + a_xt $ | $ \large v_y = v_{0y} + a_yt $ |
| $ \large x = \frac {1}{2} (v_{0x} + v_x)t $ | $ \large y = \frac {1}{2} (v_{0y} + v_y)t $ |
| $ \large x = x_0 + v_{0x}t + \frac {1}{2} a_x t^2 $ | $ \large y = y_0 + v_{0y}t + \frac {1}{2} gt^2 $ |
| $ \large {v_x}^2 = {v_{0x}}^2 + 2a_x(x - x_0) $ | $ \large {v_y}^2 = {v_{0y}}^2 + 2a_yy $ |
We can represent $ \small \overrightarrow{\normalsize x} $ and $ \small \overrightarrow{\normalsize y} $ vector components with free body diagrams, a method commonly used to solve Newton’s laws problems. We will get more into this when we study dynamics. For now, it’s important to understand that some problems must be broken into x and y components. For example, when a cart goes down a ramp, it experiences motion in the x and y directions. Its motion depends on the net acceleration in the x-direction along the ramp. Because there is a component of the acceleration due to gravity that is accelerating the cart down the incline, part of the acceleration due to gravity is vertical. Below, you will find a vector diagram of a Smart Cart that breaks its motion into x and y components.
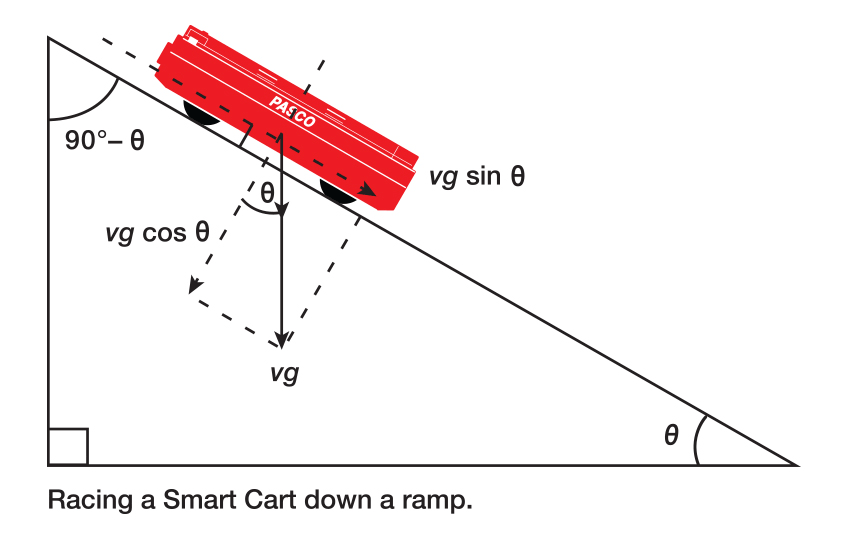
The magnitudes of the components of displacement along the axes are x and y. The magnitudes of the components of the velocity, $ \large v $ , are $ \large v_x = v\cos \Theta $ and $ \large v_y = v\sin \Theta $, where $ \large v $ is the magnitude of the velocity and theta is its direction.
Write down our known values $ \Theta = 45^{\circ} $ and $ \Delta x = 5.0 \textrm m $
We can start by taking the fourth Kinematics Equation $ {v_x}^2 = {v_{0x}}^2 + 2a_x( x - x_0) $ and rearranging it into $ {v_x}^2 - {v_{0x}}^2 = 2a_x \Delta x $
From the diagram, we see that the acceleration along the ramp is $ g \sin \Theta $. Plug $ g \sin \Theta $ and our known values into the equation and solve.
$ \Large {v_x}^2 = 2[(9.81 \textrm {m/s}^2)(\sin45^{\circ})] (5.0 \textrm m) = 8.3 \textrm {m/s} $
Teaching Tools
Wireless Smart Cart
The Wireless Smart Cart is a next-generation dynamics cart with built-in sensors that measure its position, velocity, acceleration, force and rotation. Fully functional with or without a track, the Wireless Smart Cart provides students with real-time motion data, interactive graphs, and intuitive analysis features on any device with a Bluetooth connection and PASCO software. From introductory experiments in linear and rotational motion, to Newton’s laws and multi-cart collisions, the Wireless Smart Cart enhances classic experiments and enables students to explore a new world of experimental opportunities.
Smart Cart Vector Display
The Smart Cart Vector Display brings new life to vector demonstrations with live vector displays for the velocity, acceleration and force of a Smart Cart in motion. As the cart moves, the Vector Display illuminates arrows to indicate the direction and magnitude of the cart’s motion. This innovative design enables students to observe velocity, force and acceleration vectors in real-time as the cart rolls down an incline, free falls, spins in rotation, or collides with another cart.
Learn more about the right dynamics cart and track system setup for your classroom.

Projectile Motion
Projectile Motion occurs when the only acceleration experienced by an object in flight is caused by gravity, which pulls it downward. The object in motion is called a projectile, and its path is known as its trajectory. The horizontal distance covered by a projectile is called its range. The final location minus the initial location of a projectile is called its displacement, s. Two-dimensional projectile motion problems often assume air resistance and friction are negligible. Since the motions along a perpendicular axis are independent, we can analyze them separately by breaking them into their x and y components. When we apply the kinematic equations for each component, we use the x and y subscripts to denote each variable’s relation to the x- or y-axes. For both x and y components, acceleration is constant, which allows us to use the kinematic equations.
$ \Large a_y = g = -9.81 \textrm {m/s}^2 $
Here, we are assigning the upward y direction as positive, so a projectile experiencing the force of gravity, which pulls it in the downward y direction, will experience a negative velocity. Because a projectile is only affected by gravity, there is no acceleration in the x direction.
$ \large a_x = 0 \textrm {m/s}^2 $
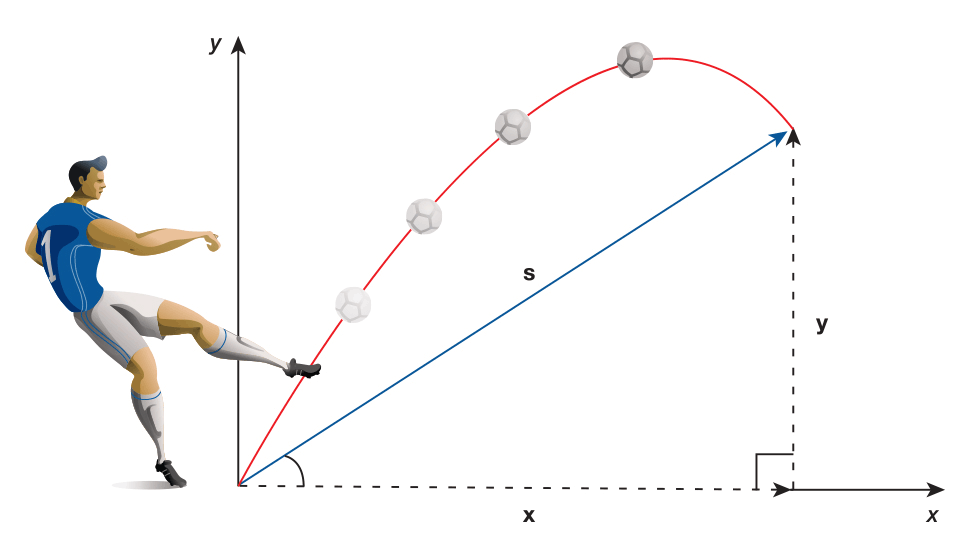
A visual representation of the total displacement, $ \Large s $, of a projectile ball at a point along its path is shown above. The vector $ \Large s $, has components $ \Large x $ and $ \Large y $ along the axes. Its magnitude makes an angle $ \Theta $ with the horizontal. Notice that $ \Large s $ and $ \Large x $ can both denote displacement. Here, we are using $ \Large s $, to simplify each vector’s identification. We can use a series of steps to analyze projectile motion.
Step 1: Break the motion into horizontal and vertical components along the x- and y-axes.
$ \large A_x = A\cos\Theta $$ \large A_y = A\sin\Theta $
The magnitudes of the components of displacement along the axes are $ \large x $ and $ \large y $. The magnitudes of the components of the velocity, $ \Large v $, are $ \Large v_x = v \normalsize \cos\Theta $ and $ \Large v_y = v \normalsize \sin\Theta $, where $ \Large v $ is the magnitude of the velocity and theta is its direction.
Step 2: Use the kinematic equations to analyze the components as two independent, one-dimensional motions. The kinematic equations for horizontal and vertical motion are below.

Horizontal Motion:
$ \large a_x = 0 \textrm {m/s}^2 $
$ \large x = x_0 + v_{0x}t $
$ \Large v_x = v_{0x} $
Vertical Motion: $ a_y = g = -9.81 \textrm {m/s}^2 $
$ \large y = y_0 + \frac {1}{2}(v_{0y} + v_y)t $
$ \large v_y = v_{0y} - gt $
$ \large y = y_0 + v_{0y}t - \frac {1}{2} gt^2 $
$ \large {v_y}^2 = {v_{0y}}^2 - 2g(y - y_0) $
Step 3: Solve for the unknowns in the horizontal and vertical directions. Remember, both variables share the time variable.
Step 4: Recombine the two motions to determine the total displacements and velocity, $ \Large v $. Because these motions are perpendicular, we can determine these vectors by using the following vector summation methods.
$ \large A = \sqrt{{A_x}^2 + {A_y}^2} $ where $ \large \Theta = \tan^{-1} (A_y/A_x) $
We can use vector summation to determine the total displacement and velocity where $ \large \Theta $ is the direction of the displacement, and $ \large \Theta_v $ is the direction of the velocity.
$ \Large s = \sqrt{x^2 + y^2} $ and $ \large \Theta = \tan^{-1} (y/x) $
$ \Large v = \sqrt{{v_x}^2 + {v_y}^2} $ and $ \large \Theta_v = \tan^{-1} (v_y/v_x) $
When we consider the horizontal and vertical components of motion, we find the horizontal motion to be simple, because $ \large a_x = \normalsize 0 $ and $ \large v_x $ is constant. The velocity in the vertical direction begins to decrease as the object rises. At its height, the vertical velocity of the object is zero. As it falls back down, the vertical velocity increases in magnitude but in the opposite direction as its initial path. The x- and y-motions are recombined to find the total velocity at any given point during the projectile’s trajectory.
Teaching Tools
Projectile Launchers
Demonstrate the independence of x- and y-motion, while helping students develop working knowledge of the kinematic equations with PASCO’s highly accurate and repeatable Mini Projectile Launcher. The Mini projectile Launcher produces highly repeatable ball launches that enable students to investigate projectile motion by comparing the effects of different launch angles and velocity on the ball’s projectile range.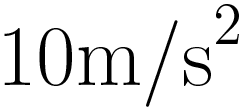 .
If the table is 3.0 m high, how far will the marble travel before the Smart Gate measures it hitting the ground?
.
If the table is 3.0 m high, how far will the marble travel before the Smart Gate measures it hitting the ground?
We’re looking to find the distance in the horizontal direction and we’re given:
$ \large v_x = v_0 = \normalsize 10 \textrm {m/s} $$ \large x = v_0t $$ \large h = \normalsize 3.0 \textrm m $
We’ll use an equation in terms of y first. $ \large y = y_0 + v_{0y}t - \frac {1}{2}gt^2 $
Since the object starts from rest, we know that $ \large v_{0y} = 0 $ and $ \large v_y = -gt $
We can simplify the equation $ \large y = y_0 + v_{0y}t - \frac {1}{2}gt^2 $ because there is no initial velocity in the y direction.
When we plug in $ \Large v_{0y} = \normalsize 0 $ we get $ \large y = y_0 - \frac {1}{2}gt^2 $
We will use this equation in y to solve for the time. Substituting h for y gives us the equation $ \large h = h - \frac {1}{2}gt^2 $
When we rearrange to solve for time, the equation becomes $ \large t = \sqrt \frac {2h}{g} $
Then, we can calculate the displacement using our equation for $ \large t $, the $ \large x $ equation, $ \large x = v_0t $, and our known values.
$ \large x = v_0t = v_0 \sqrt \frac {2h}{g} = (10 \textrm {m/s}) \sqrt \frac {2(3.0 \textrm m)}{9.81 \textrm {m/s}^2} = 7.8 \textrm m $
We are looking to find $ \Large v_{0y} $ and our known values are $ \Large v_{0x} = \normalsize +3.0 \textrm {m/s} $ and $ \Large x = \normalsize 15 \textrm m $
We’ll use the horizontal component to find the shared value, time. Then we can rearrange the equation, $ \large x = x_0 + v_0t $ so that it becomes $ \large t = \frac {x}{v_{0x}} = \frac {15}{3.0 \textrm {m/s}} = \normalsize 5.0 \textrm s $
When we consider the vertical component of the motion, we can make the downward direction negative, which means $ \large a_y = \normalsize -9.81 \textrm {m/s}^2 $. We also know there isn’t any displacement in the vertical direction, so $ \large y = \normalsize 0 \textrm m $.
$ \Large y = v_{0y}t + \frac {1}{2} a_y t^2 $ becomes $ \Large 0 = v_{0y} t + \frac {1}{2}a_y t^2 $
Plug in our value for gravity and the calculated value for time to solve.
$ \Large v_{0y} = - \frac {1}{2} a_yt = - \frac {1}{2}(-9.81 \textrm {m/s}^2)(5.0 \textrm s) = 25.0 \textrm {m/s} $
Suggested Related Topics
Rotational Motion
The kinematics of rotational motion describes the relationships between angular velocity, rotation angle, angular acceleration, and time. Each of the kinematic variables for linear motion have a rotational motion counterpart. Like linear kinematic equations, the equations for rotational motion use subscripts to denote initial values, and exclude subscripts to denote final values. Below, you will find the equations for rotational motion and their translational, linear motion equations.
| Rotational | Translational |
|---|---|
| $ \Large \Theta = \bar\omega t $ | $ \LARGE x= \bar v t $ |
| $ \Large \omega = \omega_0 + \alpha t $ | $ \Large v = v_0 + at $ |
| $ \Large \Theta = \omega_0 t + \frac {1}{2} \alpha t^2 $ | $ \Large x = v_0 t + \frac {1}{2} at^2 $ |
| $ \Large \omega^2 = {\omega_0}^2 + 2 \alpha \Theta $ | $ \Large v^2 = {v_0}^2 + 2ax $ |
Straight-Line Motion of Charged Particles in Magnetic Fields
The first Newton’s law of motion states that if an object experiences no net force, then its velocity is constant. When a charged particle’s velocity is parallel to the magnetic field, it experiences no net force and moves in a straight line through space. This is known as straight-line motion. If the velocity vector is neither parallel nor perpendicular to the magnetic field, the velocity component that is parallel to the field will remain constant.
Rolling Objects with Different Moments of Inertia
One classic high school physics question involves two cylinders. The question states: You have two cylinders, one hollow and one solid, with identical masses and diameters. If you roll them both down a slope, which cylinder will reach the bottom first?
When we roll an object, its kinetic energy takes two forms: translational (motion in a straight line) and rotational (spinning). Translational energy with constant acceleration can be described using kinematic equations, but to answer our question, we must focus on rotational inertia. Rotational inertia depends not only on the mass and rotational speed of an object, but also on how mass is distributed around the axis of rotation. This means that a hoop will have more rotational inertia than a cylinder of equal mass at the same angular velocity, because the mass in the hoop is moving faster due to its greater distance from the axis of rotation.
The quantity of rotational inertia possessed by an object is called its moment of inertia. An object’s moment of inertia can also be considered to be a measurement of how “spread out” its mass it. The equation for an object’s moment of inertia is$ I = mr^2 $, where $ I $ is equal to the moment of inertia, $ \large m $ is equal to the object’s mass, and $ \large r $ equals the radius. When two cylinders have different diameters but equal masses, the cylinder with the largest diameter will have a larger moment of inertia. Now, consider our original question. The hollow cylinder has the same mass and diameter as the solid cylinder, but its mass is more “spread out”, which causes it to have a bigger moment of inertia. So, does the magnitude of an object’s moment of inertia determine whether it will reach the bottom first? Not necessarily. In fact, if you roll the two cylinders down a ramp, the solid cylinder will reach the bottom first every time. It might seem counterintuitive, because the hollow cylinder has a larger moment of inertia, but a solid cylinder or sphere will always reach the bottom before a hollow object, regardless of diameter.
Planetary Orbits (Kepler’s Laws)
In the 16th-century, German astronomer, Johannes Kepler announced his three laws of planetary motion. The laws state: (1) All planets move about the Sun in elliptical orbits with the sun at one focus. (2) A radius vector joining any planet to the Sun sweeps out equal areas in equal lengths of time. (3) The squares of the sidereal periods of revolution of the planets are directly proportional to the cubes of their mean distances from the Sun.
These laws would eventually lend help to the development of Newton’s laws when he formulated the law of gravitation, in which he described the gravity between Earth and the Moon, as well as the Sun and the planets. Newton came to discover that the motion of bodies subject to central gravitational force don’t always follow the same elliptical orbits declared by Kepler’s first law. Instead, their paths are defined by the total energy of the body, allowing these bodies to follow hyperbolic or even parabolic orbits. Perhaps the most interesting aspect of Kepler’s laws is that they also apply to all other inverse-square-law forces, including electromagnetic forces within the atom (when proper allowances are made for relativistic and quantum effects).

Escape Velocity
Escape velocity is the speed that an object needs to be traveling to break free of a planet or moon’s gravity well and leave it without further propulsion. For example, an object on the moon must reach a speed of 2.38 km/sec to escape the moon’s gravity well. For comparison, an object on the Sun would need an escape velocity of 618 km/sec!
Satellite Orbits
Satellites are held within three types of Earth orbits in space. The high Earth orbit is farthest away from the Earth’s surface and is the location of many weather and communications satellites. The medium, or mid, Earth orbit includes navigation and most specialty satellites, and the low Earth orbit is where most scientific satellites orbit. The distance between the satellite and Earth’s surface, also known as the height of the orbit, determines the satellite’s orbital speed. The higher a satellite’s orbit is, the slower it will move. Other factors that influence a satellite’s orbit include eccentricity and inclination.




